Funkcie

Funkcia je predpis, ktorý jednému $x$ priraďuje najviac jedno $y$. Zvyčajne $x$ a $y$ predstavujú čísla z $R$.

$f(x) = y$

Funkciu môžeme zapísať rôznymi spôsobmi: $f(x) = y$, $y = x$

Teória

Definičný obor

Definičný obor funkcie je množina hodnôt, ktoré môžeme dosadiť za $x$.

Označujeme ho $D(f)$.

Obor hodnôt

Obor hodnôt predstavuje množinu všetkých hodnôt, ktoré môže nadobúdať $y$.

Označujeme ho $H(f)$.

Vlastnosti funkcií

Párnosť

Funkcia je párna práve vtedy, keď $f(x) = f(-x)$, teda vtedy, keď je graf súmerný podľa y-ovej osi (zvislá).

Príkladom párnej funkcie je kvadratická funkcia $f(x) = x^2$.

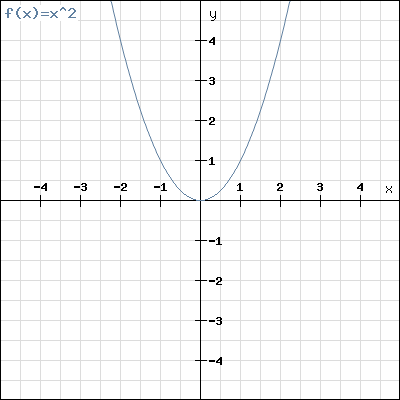
Funkcia je nepárna práve vtedy, keď $f(-x) = -f(x)$, teda vtedy, keď je graf súmerný podľa počiatku súradného systému.

Príkladom nepárnej funkcie je funkcia $f(x) = x^3$.

Funkcia nemusí byť len párna alebo nepárna. Môže nebyť ani párna, ani nepárna. Pre takúto funkciu neplatí ani $f(x) = f(-x)$, ani $f(-x) = -f(x)$.

Príkladom ani párnej, ani nepárnej funkcie je funkcia odmocniny $f(x) = \sqrt{x}$. Funkcia odmocniny nie je súmerná ani podľa y-ovej osi (zvislá), ani podľa počiatku súradného systému.

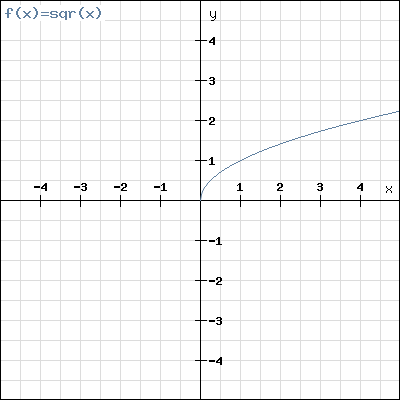
Monotónnosť

Prostosť

Funkcia je prostá, keď $x_1, x_2 \in D(f); x_1 \neq x_2; f(x_1) \neq f(x_2)$.

Funkcia je prostá, keď pre ľubovoľné dve $x_1, x_2$ z $D(f)$, ktoré nie sú rovnaké, platí, že ich funkčné hodnoty sa nerovnajú.

Ak je funkcia prostá, existuje pre ňu jej inverzná funkcia.

Príkladom prostej funkcie je lineárna funkcia alebo funkcia $f(x) = x^3$.

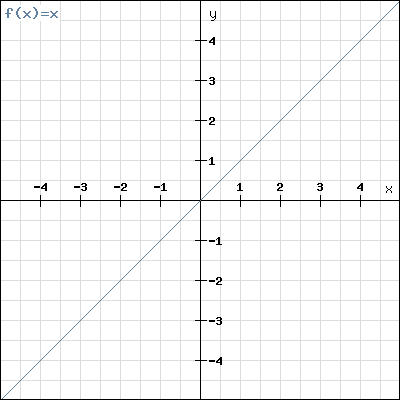
Príkladom funkcie, ktorá nie je prostá je kvadratická funkcia.

Ohraničenosť

Extrémy

Periodickosť

Graf

Príklady

Príklady funkcií: $f(x): \frac{x+4}{x+5}$